En esta condición podemos limitar por dos diferentes conceptos, la probabilidad de cada apuesta y/o la Relación entre Premio y el Coste (RPC). Cada uno de ellos es opcional, es decir, se puede utilizar uno, el otro, o los dos.

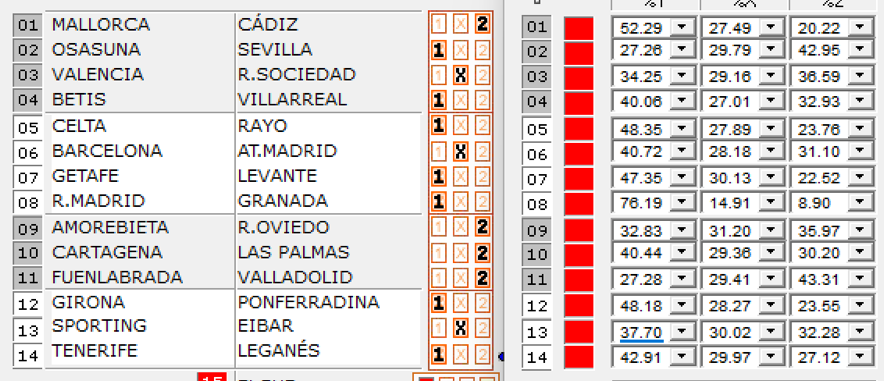
Cada apuesta tiene una determinada probabilidad de conseguir un premio de 14,13,12,11 ó 10 y podemos condicionarnos a jugar las apuestas que tengan un límite concreto de probabilidad. Dicha probabilidad se calcula según los signos de la apuesta y la probabilidad real de cada uno de ellos. Por ejemplo, en la siguiente imagen vemos una apuesta y los porcentajes de probabilidad real que tienen los signos de cada partido.

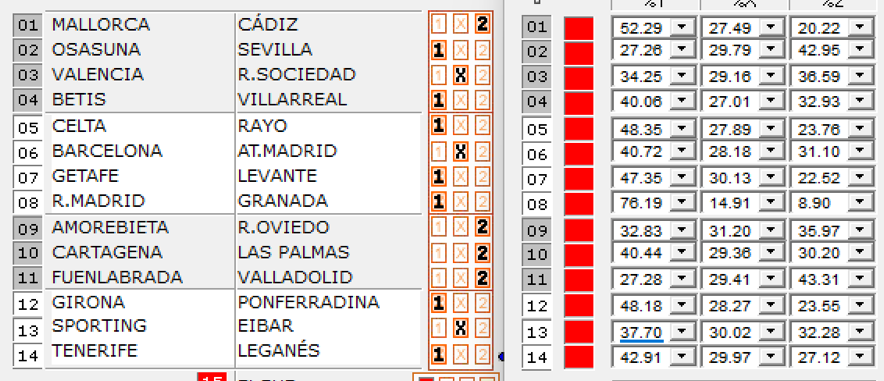
En la casilla 1 tenemos el 2, que tiene una probabilidad del 20,22%. En la casilla 2 tenemos el 1, que tiene un 27,26%. En la casilla 3 tenemos la X, que tiene un 29,16% y así sucesivamente hasta la casilla 14. Para obtener la probabilidad real de la apuesta tenemos que multiplicar la probabilidad de cada signo en tanto por 1, que sería:
0,2022*0,2726*0,2916*0,4006*0,4835*0,2818*0,4735*0,7619*0,3597*0,3020*0,4331*0,4818*0,3002*0,4291
Y nos daría un resultado de 0,000092412869, que es la probabilidad real que tiene esta apuesta para ser convertirse en un premio de 14 (que salgan los 14 resultados).

Dicha apuesta, a parte de la probabilidad de acertar 14, también tiene su probabilidad de quedarse con 13,12,11 ó 10. El cálculo se realiza de la misma forma pero aplicando cambios según la categoría de premio esperada. En este caso, la apuesta tiene las siguientes probabilidades:
0,000092412869 al 14
0,002376702537 al 13
0,027864657940 al 12
0,197360606440 a 11
0,943131434115 al 10
Entendiendo que cada apuesta tiene su propia probabilidad real de conseguir cada determinada categoría de premio, también se entiende que todas las apuestas tienen probabilidades diferentes. Por lo tanto, podemos limitar las apuestas que queremos jugar según sus probabilidades de obtener premio.

Al entrar en la condición de PROBABILIDAD DE APUESTAS / RPC, primero encontramos un cuadro para seleccionar los porcentajes:

• • %Apostados. Por defecto se seleccionan los porcentajes LAE pero también se pueden seleccionar los apostados en Quinielista, Medias de ambos, o porcentajes propios.
• • %Reales. Por defecto se seleccionan los porcentajes de Probabilidad Real obtenidos de casas de apuestas, también se pueden seleccionar del Análisis de Quinielista, Medias entre jugados LAE / Quinielista, o porcentajes propios.

Se pueden modificar accediendo por el icono de la Lupa. Cada vez que se modifican el programa tarda unos segundos en calcular las probabilidades con los porcentajes seleccionados.

Luego tenemos los cuadros de los límites mínimos y máximos que se encuentran en todas las apuestas de la combinación calculada.

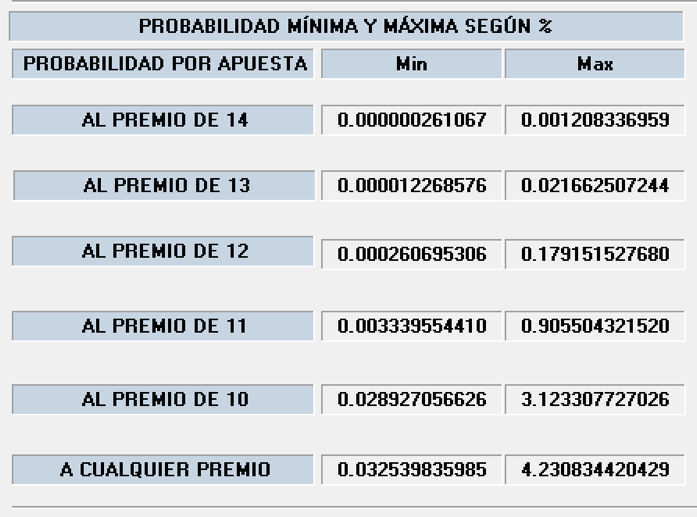
En la imagen vemos que, en la jornada 36 de la temporada 2021/22, tomando como referencia los porcentajes reales, tenemos probabilidades que van desde el 0,000000261067 hasta el 0,001208336959 para el 14. Es decir, la apuesta que tiene una menor probabilidad al 14 es del 0,000000261067 y la que tiene una mayor probabilidad es del 0,001208336959. Entre estas, tenemos diferentes cantidades para cada una de las 4.782.969 apuestas posibles en el pronóstico de los 14 triples.

Lo mismo podemos observar para las probabilidades de las diferentes categorías de premio (13,12,11,10). Y también para la probabilidad A CUALQUIER PREMIO, en este caso, para cada apuesta se calcula la suma de las probabilidades para cualquiera de las diferentes categorías de premio.

Cabe tener en cuenta que, aunque hay pequeñas diferencias, en general, si pedimos las apuestas con mayor probabilidad al 14 también serán las que tengan mayor probabilidad al 10. Podemos limitar una, varias, o todas las categorías, pero siempre teniendo en cuenta que pueden solaparse unas con otras.

Para establecer el límite de una categoría podemos ir directamente a las casillas de la derecha para indicar el mínimo y/o el máximo. O podemos hacer clic en la flecha azul para consultar y “traspasar” los limites según sus probabilidades. Veamos un ejemplo si pulsamos en la flecha azul del premio de 14:

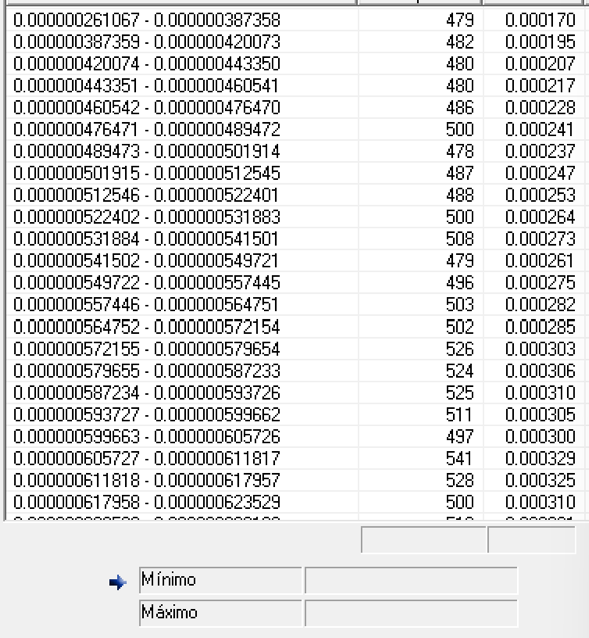
Nos aparece una ventana donde se agrupan los límites de todas las apuestas en diferentes rangos o grupos. En la primera línea de arriba vemos indicado que entre 0,000000261067 y 0,000000387358 existen un total de 479 apuestas y el conjunto de estas apuestas ofrecen una probabilidad del 0,000170 de conseguir el 14 en alguna de sus apuestas.

Si ahora bajamos con el scroll hasta el final de la lista, veremos lo siguiente:

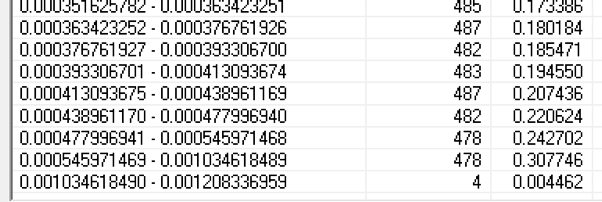
Si miramos la última línea, vemos que entre los límites entre 0,001034618490 y 0,001208336959 existe un total de 4 apuestas que, en su conjunto, nos ofrecen una probabilidad del 0,004462% de conseguir el 14.

Cabe tener en cuenta que las primeras tienen mucha menos probabilidad pero también el importe del premio será mucho mayor que en las últimas. Será cuestión de encontrar cierto equilibrio.

Siguiendo dentro de esta utilidad, falta saber que podemos seleccionar varios límites de forma correlativa, no pueden ser saltados, para ello, hacemos clic en un primer límite de arriba y luego hacemos clic en un segundo límite de abajo, automáticamente quedarán seleccionados todos los límites entre uno y otro. En la parte inferior observaremos el límite desde/hasta que hemos seleccionado, la cantidad de apuestas que contiene, y la probabilidad que tenemos de obtener el 14 con las apuestas que entran en el límite seleccionado.

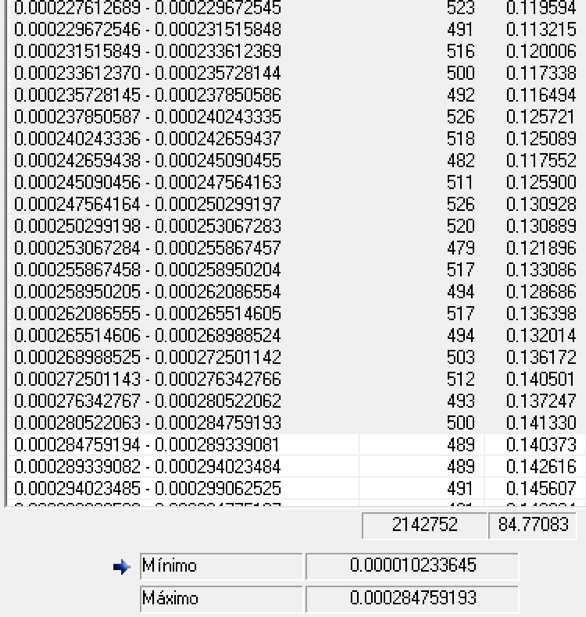
Al final, si pulsamos el botón OK, volveremos a la pantalla anterior y los límites ya nos aparecerán seleccionados en la condición

A tener en cuenta.

• • - En estos ejemplos teníamos una combinación con todas las apuestas de los 14 triples. Si hubiéramos tenido otras condiciones establecidas, los datos de la ventana sólo serían sobre las apuestas de la combinación establecida. Es decir, si nuestra combinación era de 150 apuestas, los grupos se hubieran mostrado divididos entre 150 apuestas y no sobre el total de los 14 triples.
• • - La misma aplicación de esta ventana se establece para seleccionar apuestas sobre las diferentes categorías de premio (14,13,12,11,10)

Existe una relación entre la probabilidad de que una apuesta acierte el 14 y el importe de dicho premio de 14, en base a ella, se puede establecer si dicha apuesta puede ser más o menos rentable. A este concepto lo llamamos RPC – Relación Premio Coste.

La siguiente apuesta, que ya hemos calculado en un ejemplo anterior, nos ofrece una probabilidad del 0,000101792037 de acertar el14.

Si dividimos 100 entre 0,000101792037 tenemos un resultado de 982395. Eso, en teoría, quiere decir que tendríamos que jugar 982395 veces dicha apuesta para alcanzar un 100% de probabilidades al premio de 14.
Jugar 982395 veces dicha apuesta a 0,75 euros cada vez, nos costaría un total de 736796 euros. Con esto, tenemos la variable del COSTE que tendríamos para acertar un 14 con dicha apuesta.

Por otro lado, tenemos que calcular la variable del PREMIO que podría ofrecernos. Si hacemos una estimación con los porcentajes jugados según LAE, esta apuesta podría darnos un premio de 14 de 26846 euros. Evidentemente, tener que gastar 736796 euros para, algún día, cobrar un 14 de 26846 euros no nos saldría muy a cuenta.

Si dividimos la variable del PREMIO entre la del COSTE, tendríamos 26.846/736796=0,03644. La relación ideal sería superior a 1, así que con 0,03644 estamos tan lejos como muestra el tener que gastar 736796 euros para cobrar 26.000 euros.

Vamos a ver otro ejemplo con la siguiente apuesta:

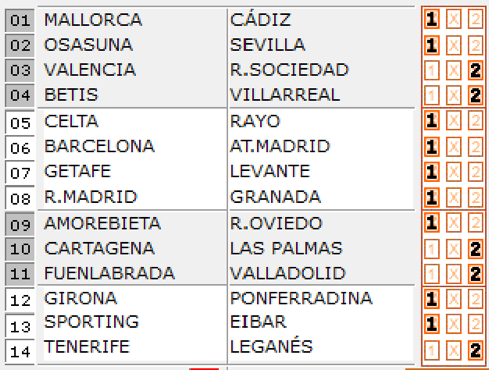
Su probabilidad al 14 es del 0,000289131628
Si dividimos 100 entre 0, 000289131628 tenemos que habría que jugarla 345863 veces para llegar al 100% del 14. Lo que supondría una variable COSTE de 345863*0,75 = 259397 euros.

Si ahora calculamos la estimación del premio de 14. Tenemos la variable PREMIO por un importe de 483235 euros.

Ya se observa que nos ofrece un premio mayor que su coste. Si dividimos PREMIO / COSTE, 483235 / 259397 tenemos una Relación Premio/Coste (RPC) del 1,88254

Al estar por encima de 1, significa que cobrará más que lo que costará, por lo tanto esta apuesta sí resulta interesante.

¿Es 1 el RPC mínimo que deberíamos considerar?

No es necesario. 1 es la referencia teórica pero cabe tener en cuenta otras variables.
Si esta apuesta la jugáramos 345863 veces, es evidente que, por el camino, acertaríamos premios de 10,11,12,13 que rebajarían el coste de 259397 euros. Si contamos que los premios de 10,11,12,13 reciben el 9%, 7.5%, 7.5%, 7.5%, de la recaudación, respectivamente, podemos calcular que con estos premios recuperaríamos sobre el 31.5% de lo jugado, por lo tanto, al coste de 259397 euros habría que restarle este 31% y nos quedaría en 179984 euros.
Por otro lado, al premio de 483235 euros habría que restarle el 20% de los impuestos, por lo tanto, nos quedarían sobre 398660 euros.
Entonces, si calculáramos el RPC de 398660 entre 179964 tendríamos un 2,21522 que es mayor al 1,88254 anterior.

También cabe tener en cuenta que cada premio de 14 lleva implícita una probabilidad al premio de 15 y que dicho premio puede cobrar más o menos según el bote que pudiera existir en una semana concreta.

En general, si jugamos el signo más probable en el P15, podemos contar con una probabilidad cercana al 11% de acertarlo. Si, también en general, estamos jugando apuestas con un rango de 14 de 0 a 10, es lógico que si acertamos el 15 sea único.

El P15 recibe el 7.5% de la recaudación, que vienen a ser unos 240.000 euros sin contar el Bote. Si tenemos un 11% a dicho premio, podemos contar con que podemos sumar 26.400 euros a la variable PREMIO. Con lo que el RPC nos quedaría en (425060/179964) = 2,36192.

Es decir, aunque el cálculo teórico inicial del RPC fuera de 1,88254 si tenemos en cuenta las variables de arrastres de premios inferiores, impuestos sobre premios superiores y probabilidad al premio de 15 (sin bote), el RPC final sería de 2,36192. Un 25% mayor.

Esto quiere decir que el RPC ideal podría empezar a contarse desde 0,8 en lugar de 1,0.

¿Entonces, cual podría ser un RPC ideal para condicionar nuestra combinación?

• En términos teóricos sería de 0,8 (incluso algo menor en las jornadas con bote).
• En términos de “querer apretar” podríamos subir hasta 1,0.
• En términos “conservadores” podríamos bajar hasta 0,65.
• En términos de querer utilizar la condición muy “suavemente” para que elimine apuestas sin “entorpecer” demasiado con jugar un mínimo entre 0,15 y 0,20 nos estaríamos quitando las peores apuestas, y suelen ser bastantes.

Cabe tener en cuenta:

• Que los cálculos sobre una única apuesta nos ofrecen cifras un tanto impensables. Es decir, tener que jugar una apuesta medio millón de veces (o jornadas) no puede considerarse un escenario real.
• El efecto de la condición se normaliza si tenemos en cuenta que en nuestra combinación no jugamos sólo una apuesta, sino decenas, cientos, o miles, que acumulan y equilibran los resultados de unas con otras.
• Que cuando la teoría dice que “se acierta 1 vez cada 100.000”, la vez puede ser la número 1 o la número 100.000. Cosa impredecible dentro de un ciclo real.
• Que, en teoría, podemos calcular con un 33% de desviación. Es decir, un “1 de 100.000” puede estar entre el “1 de 67.000 como en 1 de 133.000”.
• Que cuando calculamos la estimación del PREMIO sólo es una estimación. Puede pasar que en una estimación de que saldrán 2 premios de 14 que han de cobrar 240000 euros cada uno, resulte que no salga ninguno (cobraría 480.000) o que salgan 3 o 4 (cobrarían entre 120.000 y 160.000).